(Contribución de El neutrino a la edición 5.5: Ronald Fisher del Carnaval de Matemáticas, organizada por pimedios | La aventura de las matemáticas)
Cuando en casa compramos fresas, me suele tocar a mí prepararlas. Y eso que no las como. Pero así es la vida. El caso es que soy yo el encargado de cortarles las hojas y de partirlas en trozos, que intento que sean lo más iguales posible. Lo que no es fácil, dada la forma de este fruto. Que no es estrictamente un fruto; en realidad es el receptáculo de la flor, el extremo del pedúnculo en el que se insertan los sépalos y los pétalos. Si por algo yo no las como... Los verdaderos frutos son las motitas duras que se reparten por la superficie de la fresa; son aquenios, frutos secos monocarpelados e indehiscentes, o sea, que proceden cada uno de un solo pistilo o carpelo, y que no se abren al madurar. Cada aquenio contiene una semilla, que no está unida al pericarpio, la corteza que la rodea.
¿Cómo cortar una fresa en trozos de (más o menos) el mismo tamaño? Las fresas suelen tener simetría de rotación, así que si las cortamos a lo largo de su eje, longitudinalmente, como en la figura 1, el problema es trivial. La dificultad se presenta cuando la fresa es grande y queremos cortarla transversalmente, como en la figura 2. Bueno, aunque estoy hablando de fresas, a lo que me refiero en realidad es a los fresones, que es lo que se vende en la gran mayoría de las fruterías, por lo menos en las que yo frecuento. Las verdaderas fresas son pequeñas y más redonditas, así que no tiene mucha dificultad cortarlas.
 |
 |
| (figura 1) Fresa cortada longitudinalmente (Forest & Kim Starr, 2008) |
(figura 2) Fresas cortadas transversalmente (Darkon X, 2010) |
Entonces, el problema al que nos enfrentamos es éste: ¿cómo cortar una fresa o fresón transversalmente en dos partes iguales? Como físico que soy, voy a hacer algunas aproximaciones. La forma de un fresón, sobre todo después de cortarle las hojas, se puede aproximar, con un poco de buena voluntad, a la de un cono. Más o menos. En realidad, es una forma intermedia entre un cono y un cilindro, pero cortar un cilindro en dos partes iguales transversalmente también es muy fácil, simplemente se corta por la mitad. Así que seguimos adelante con el cono.
El volumen de un cono de altura H y base de radio R es
 |
| (figura 3) Triángulos semejantes |
Esto es equivalente a
La proporción entre la altura y el radio de la base es la misma en los dos conos. Si despejamos R = H/k (y r = h/k), podemos expresar el volumen como
Como no necesitamos conocer el valor absoluto del volumen de la fresa, ya que sólo nos interesa la proporción entre el volumen del cono pequeño y el del cono grande, podemos agrupar todas las constantes del problema en una constante
y así el volumen nos queda K · H3 para el cono grande, y K · h3 para el cono pequeño.
No se me ha olvidado, lo que queremos es cortar la fresa en dos trozos iguales, así que el volumen del cono grande, la fresa entera, tiene que ser el doble del volumen del cono pequeño, el trozo que cortamos.
O lo que es lo mismo,
O sea, que hay que cortar la fresa de manera que el cono pequeño, el trozo más estrecho, se queda prácticamente con 4/5 de la longitud de la fresa. Parece demasiado, pero la geometría no engaña. Para un cono perfecto, es así; qué engañosa puede ser nuestra apreciación de los volúmenes. Pero en el caso de una fresa es otra cosa; 4/5 sí que puede ser demasiado. Ya hemos dicho que una fresa no tiene forma de cono, sino que más bien es algo intermedio entre un cono y un cilindro. Como en un cilindro el corte hay que hacerlo por la mitad, lo más correcto para cortar la fresa será algún punto entre la mitad y los 4/5 de su longitud. Por ahí andan los 2/3 y los 3/4. Lo siento, no puedo precisar más; el punto exacto dependerá de cada fresa. Y da gracias si no se te cruza una fresa como la de la figura 4.
 |
| (figura 4) Una fresa muy difícil de cortar (KoS, 2007) |













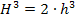



















No hay comentarios:
Publicar un comentario